Flory-Huggins Lattice Theory
of Polymer Solutions, Part 2
The classical thermodynamics of (binary) polymer solutions was first developed by Paul Flory1 and Maurice Huggins2 independently in the early 1940s. They assumed a rigid lattice framework and a regular solution (random mixing) and obtained for the free energy of mixing per unit volume following expression:
Δfmix / kT = φp / (r·vr) · ln φp + φs / vs · ln φs + χps φs φp / v
where φs and φp are the volume fractions of the solvent and polymer,
φs = Nsvs / (Nsvs + Nprvr), φp = Nprvr / (Nsvs + Nprvr)
The two parameters vs and vr are the volumes of a solvent molecule and of a polymer repeat unit with one and r repeat units respectively. The parameter v is the average segmental volume, (vrvs)1/2.
Assuming equal lattice volumes for both repeat units, as was assumed by Flory1, the free energy per lattice site can be written as
Δfmix / kT ≈ φp / r · ln φp + φs ln φs + χps φs φp
At first it was assumed that the interaction parameter χ is independent of the concentration φp. But it became soon evident that χ is a function of both the temperature T and concentration of the polymer. Furthermore, χ is also a function of the molecular weight of the polymer, not only at low but also at high polymer concentrations. However, there are quite a number of cases where χ seems to be independent of composition, i.e. good solvents, as was proposed by the original Flory-Huggins theory. Some examples are polyisobutylene (PIB) in cyclohexane and poly(dimethyl siloxane) (PDMS) in n-octane. For this situation, the prediction of the free energy of mixing and of the phase curves (binodal and spinodal) is least difficult.
Temperature Dependence of Interaction Parameter
The temperature dependence of the interaction parameter is quite obvious from the definition of the χ parameter:
χ(T) = -z/2 (εpp + εss - 2 εps) / kT = B / T
where B describes the temperature dependence of χ. According to this equation, χ is a linear function of the inverse temperature. For the case B > 0 and (very) low temperatures, the free energy curve is concave and homogenous mixtures are unstable because the second derivative of the free energy of mixing is negative and the contribution of the entropy is small.
In most cases, mixing of a polymer with a solvent results in a volume change, that is, local packing effects lead to a temperature-independent additive constant in the Flory expression for the interaction parameter. Empirically, the temperature dependence of χ is often written as a sum of two terms:
χ(T) = A + B / T
The temperature independent term A is the so-called "entropic part" of of χ, while B / T is called the "enthalpic part". The parameter A and B have been tabulated for many polymer-solvent and polymer-polymer systems.
Binodal Phase curve
The phase boundary between the single- and two-phase region, the so-called binodal, can be determined from the common tangent of the free energy of mixing at the compositions φP,B1 and φP,B2, corresponding to the equilibrium composition of the two phases:
∂Δfmix / ∂φP |φP,B1 = ∂Δfmix / ∂φP |φP,B2-
The derivative of Δfmix is
∂Δfmix / ∂φP = kT · [r -1 ln φp + r-1 - ln φs - 1 + χ (1 - 2φp)]
And for the general case of two polymers with r and s repeat units per polymer:
∂Δfmix / ∂φp1 = kT · [r -1 ln φp1 + r -1 - s-1 ln (1-φp1) - s-1 + χ (1 - 2φp1)]
For the simple case of polymers of equal length, r = s = n, the tangent is horizontal:
∂Δfmix / ∂φp1 = kT · [n -1 ln φp1 - n-1 ln (1-φp1) + χ (1 - 2φp1)] = 0
This equation can be solved for the Flory-Huggins parameter corresponding to the binodal (phase boundary):
n · χB = ln φp1 - ln (1-φp1) / (1 - 2φp1) = ln [φp1 / (1-φp1)] / (1 - 2φp1)
And with the temperature dependence of the interaction parameter, χ = A + B / T, this relation can be solved for the binodal of the phase diagram, i.e. for the binodal temperature as a function of composition:
TB = B / {ln[φp1 / (1 - φp1)] / (2 n φp1 - n) - A}
Spinodal Phase Curve
The boundary between the unstable and metastable region, the so-called spinodal, can be calculated from the inflection points of the free energy curve:
(∂2Δfmix / ∂φP2)p,T = kT {(φp r)-1 + [(1 - φp) s]-1 - 2χ} = 0
This equation can be solved for the Flory-Huggins interaction parameter corresponding to the spinodal phase boundary:
χS = ½ {(φp r)-1 + [(1 - φp) s]-1}
The spinodal phase boundary can also be written as a temperature-composition relation:
TS = B / {(2φp r)-1 + [2(1 - φp) s]-1 - A}
In a binary blend, the lowest point of the spinodal corresponds to the critical point4:
χc = ½ · (r -½ + s-½)2
or
Tc = B / (χc - A) = B / {½ · (r -½ + s-½)2 - A}
For a symmetrical polymer mixture, r = s = n, the whole phase curve becomes symmetric with the critical point:
χc = 2 / n and φc = 1/2
whereas in polymer solutions, r = n and s = 1, the whole phase curve becomes very asymmetrical with the critical point:
χc ≈ ½ + 1 / n½ and φc = 1 / n½
Spinodal and Binodal Phase Diagram
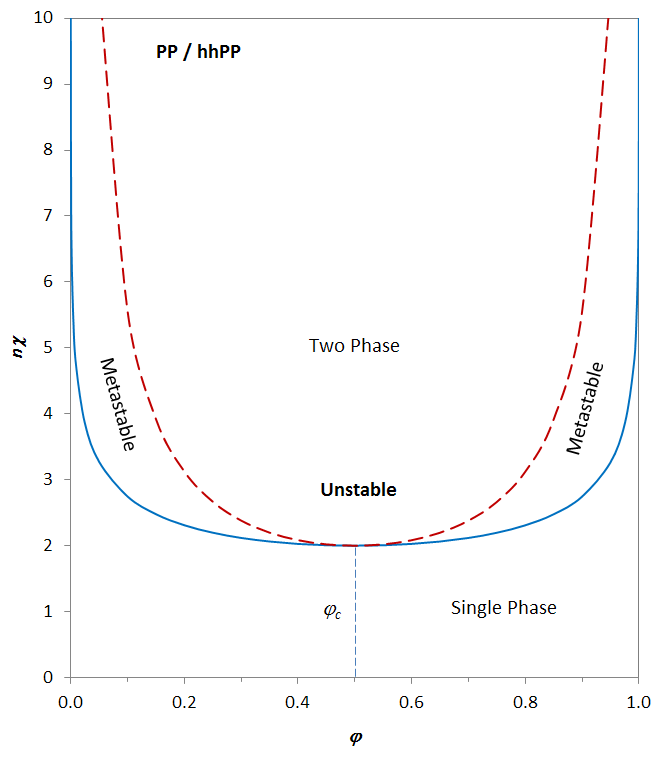
Spinodal and Binodal Phase Diagram
The figure above shows the product n χ as a function of polymer concentration φp for a symmetrical blend of polypropylene (PP) and head-to-head polypropylene (hhPP). The binodal (solid curve) and spinodal (dashed curve) have been calculated with the equations above and the parameters A = -0.0036 and B = 1.84. The two curves coincide at the critical point.
References and Notes
- P. J. Flory, J. Chem. Phys. 9, 660 (1941); 10, 51 (1942)
- M. L. Huggins, J. Phys. Chem. 46, 151 (1942); J. Am. Chem. Soc. 64, 1712 (1942)
- Paul L. Flory, Principles of Polymer Chemistry, Ithaca, New york, 1953
- Note, the spinodal and binodal of any binary mixture meet at the critical point.